Understanding Copulas

In statistics, copulas are functions that allow us to define a multivariate distribution by specifying their univariate marginals and interdependencies separately. In modelling returns of assets, for example, this enables greater flexibility and ability to model joint behaviour in extreme events.

Let’s study this in further detail using daily log returns of two assets, Apple and Goldman Sachs, over a 12-year period.

library(tseries)
options("getSymbols.warning4.0"=FALSE)
a <- get.hist.quote(instrument = 'AAPL',
                    start="2009-01-04", end="2021-01-04",
                    quote = c("AdjClose"), provider = "yahoo",
                    compress = "d")
b <- get.hist.quote(instrument = 'GS',
                    start="2009-01-04", end="2021-01-04",
                    quote = c("AdjClose"), provider = "yahoo",
                    compress = "d")
df <- data.frame(list(diff(log(a)), diff(log(b))))
colnames(df) <- c('aapl', 'gs')

time series starts 2009-01-05
time series ends   2020-12-31
time series starts 2009-01-05
time series ends   2020-12-31

Let’s take a peek at the top 10 rows of the dataframe.

print(head(df[1:10,], 10))

                  aapl            gs
2009-01-06 -0.01663156 -0.0007888361
2009-01-07 -0.02184523 -0.0486211860
2009-01-08  0.01839934  0.0107118530
2009-01-09 -0.02313506 -0.0175993365
2009-01-12 -0.02142469 -0.0773947112
2009-01-13 -0.01077318  0.0032132961
2009-01-14 -0.02750955 -0.0290366487
2009-01-15 -0.02311758 -0.0248805384
2009-01-16 -0.01267316 -0.0106212447
2009-01-20 -0.05146606 -0.2102222980

Modeling Tail Dependence

Say we want to estimate tail dependence of these assets, i.e. co-movements at the extreme ends of daily returns. In other words, what is the chance that AAPL’s worst cases are also GS’s worst cases?

Let \(\lambda\) denote the lower tail dependence of asset \(y_1\) and \(y_2\) at probability \(q\).

We first compare the tail depedencies, at various probabilities, of the empirical data and 100000 samples from a bivariate normal distribution (with its mean and covariance matrix estimated from the data).

# parameter estimates
cat('Sample mean:\n')
cat(df_means <- c(mean(df[,1]), mean(df[,2])))
cat('\n\n')
cat('Sample covariance:\n')
print((df_cov <- cov(df)))

library(mvtnorm)
set.seed(42)
# 100k samples from bivariate normal
mvn_samples <- rmvnorm(1e5, df_means, df_cov)

Sample mean:
0.001264829 0.0004185186

Sample covariance:
                aapl           gs
aapl 0.0003283744 0.0001778626
gs   0.0001778626 0.0004364080

probs <- c(0.2, 0.1, 0.05, 0.02, 0.01, 0.005, 0.001)

tally1 <- matrix(0, 2, 7)
for (i in 1:7){
    q = probs[i]
    tally1[,i] = c(
        (sum((df[,1]<quantile(df[,1], q))*(df[,2]<quantile(df[,2], q))) / 
         sum((df[,1]<quantile(df[,1], q)))),
        (sum((mvn_samples[,1]<quantile(mvn_samples[,1], q)) * 
             (mvn_samples[,2]<quantile(mvn_samples[,2], q))) 
         / sum((mvn_samples[,1]<quantile(mvn_samples[,1], q))))
    )
}

tally1_df <- as.data.frame(tally1, row.names=c('observed','normal'))
colnames(tally1_df) <- as.character(probs)
print(tally1_df)

               0.2       0.1     0.05      0.02      0.01  0.005 0.001
observed 0.4668874 0.4337748 0.397351 0.3114754 0.3225806 0.1875  0.50
normal   0.4176500 0.3066000 0.218000 0.1570000 0.1130000 0.0800  0.07

We observe as the probabilities get smaller, the calculated tail dependences between empirical returns and data sampled from the bivariate normal distribution begins to differ greatly.

Let’s try to do better with copulas.

Introducing Copulas

The term ‘copula’ is derived from the Latin for ‘link’, and in our context, is named aptly so. We can understand copulas as multivariate cumulative distribution functions that link marginal distributions and describe their interdependencies. Its marginal distributions are all Uniform(0,1), we use Uniform as a ‘bridge’ since a random variable from any distribution can be transformed to Uniform and back with the probability integral transform.

The copula of a random vector \((X_1,X_2,\ldots,X_p)\) is definined as the joint CDF of \((U_1,U_2,\ldots,U_p)\):

\((u_1,\ldots,u_p)\in [0,1]^p\), \(C(u_1,\ldots,0,\ldots,u_p)=0\), \(C(1,\ldots,1,u,1,\ldots,1)=u\), and like any other CDF, \(C\) is nondecreasing.

Some common examples include

• independence copula: \(C(u_1,u_2,\ldots,u_p)=u_1u_2\cdots u_p\)
• co-monotonicity copula: \(C(u_1,u_2,\ldots,u_p)=\min(u_1,u_2,\ldots,u_p)\)
• Gaussian copula: \(C_\Sigma^{\text{Gauss}}(u_1,u_2,\ldots,u_p)=\Phi_\Sigma\left(\Phi^{-1}(u_1),\ldots,\Phi^{-1}(u_p)\right)\)

We will be using the copula package, which has various common predefined copulas for us to choose and sample from.

Estimating Marginal Distributions

Before that, let us first fit marginal distributions for the daily returns of AAPL and GS with the help of the MASS package. fitdistr() will help us find the optimal parameters given a distribution, so let us compare between the AIC for Normal, t and Cauchy distributions.

options(warn=-1)
library(MASS)
cat('AAPL\n')
cat(paste('Normal:\t',AIC(fitdistr(df$aapl, 'normal')),'\n'))
cat(paste('t:\t',AIC(fitdistr(df$aapl, 't')), '\n'))
cat(paste('Cauchy:\t',AIC(fitdistr(df$aapl, 'cauchy')), '\n'))
cat('\nGS\n')
cat(paste('Normal:\t',AIC(fitdistr(df$gs, 'normal')),'\n'))
cat(paste('t:\t',AIC(fitdistr(df$gs, 't')), '\n'))
cat(paste('Cauchy:\t',AIC(fitdistr(df$gs, 'cauchy')), '\n'))

AAPL
Normal:	 -15645.9234978236 
t:	 -16179.9680136581 
Cauchy:	 -15654.6146727265 

GS
Normal:	 -14787.2501190948 
t:	 -15752.4739791247 
Cauchy:	 -15282.9761802124 

t distribution gives the lowest AIC, so we shall use that as our marginals. Let’s proceed to extract the optimal parameters for both assets. Note that fitdistr() uses the location-scale family, so besides the degree of freedom, location m and scale s are returned as well.

cat('AAPL\n')
(aapl_t_param <- fitdistr(df$aapl, 't'))

aapl_m <- aapl_t_param$estimate['m']
aapl_s <- aapl_t_param$estimate['s']
aapl_df <- aapl_t_param$estimate['df']

cat('\nGS\n')
(gs_t_param <- fitdistr(df$gs, 't'))
gs_m <- gs_t_param$estimate['m']
gs_s <- gs_t_param$estimate['s']
gs_df <- gs_t_param$estimate['df']

AAPL
          m              s              df     
     0.0014079306   0.0122031312   3.4246717881 
    (0.0002668132) (0.0002885762) (0.2373954742)

GS
          m              s              df     
     0.0005630129   0.0124256289   2.9726045290 
    (0.0002772650) (0.0002930408) (0.1810629562)

We’ll now transform the data into Uniform(0,1) by taking their order statistics and dividing it by the number of observations plus one. The ‘+1’ is added as a pseudo-observation so that all variates are forced inside the unit space to avoid problems with density evaluations at the boundaries. Without this, fitcopula() will throw an error.

As a side note, let’s briefly see how this works. We want to show that taking the ranks of variates \(x_1,\ldots,x_n\) and dividing it by their total count to transform them into Uniform(0,1).

With \(x_1,\ldots,x_n\), we can find a nondecreasing order \(x_{(1)}\leq x_{(2)}\leq\ldots\leq x_{(n)}\). By doing this, we are picking each variate and counting \(j\), the number of \(x_i,i\in\{1,\ldots,n\}\) less than or equals to it. Taking the proportion of \(j\) on the total count \((n+1)\), we have

Then \(u_j=\frac{1}{n+1},\frac{2}{n+1},\ldots,\frac{n}{n+1}\) which approximates \(U\sim \text{Uniform}(0,1)\).

u_aapl <- rank(df$aapl)/(nrow(df)+1)
u_gs <- rank(df$gs)/(nrow(df)+1)
u_df <- data.frame(list(u_aapl, u_gs))
colnames(u_df) <- c('u_aapl', 'u_gs')

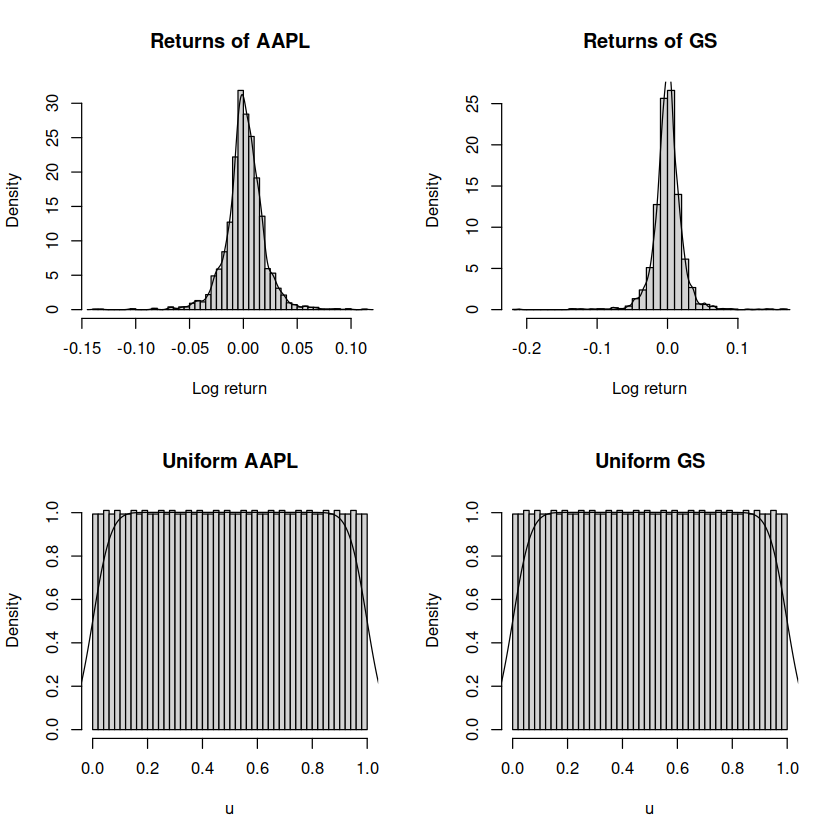
# original density of returns
par(mfrow=c(2, 2))
hist(df$aapl, freq=FALSE, breaks=50, 
     main="Returns of AAPL", xlab="Log return")
lines(density(df$aapl))
hist(df$gs, freq=FALSE, breaks=50, 
     main="Returns of GS", xlab="Log return")
lines(density(df$gs))

# transformed density of returns (uniform)
hist(u_aapl, freq=FALSE, breaks=50, 
     main="Uniform AAPL", xlab="u")
lines(density(u_aapl))
hist(u_gs, freq=FALSE, breaks=50, 
     main="Uniform GS", xlab="u")
lines(density(u_gs))

Choosing and Fitting Copulas

The copula library gives a wide selection of common copulas (elliptical and frequently-used Archimedean copulas). Fitting a few, we observe that the t copula gives us the best fit in terms of maximum pseudo-likelihood.

library(copula)
fitCopula(normalCopula(dim=2), data=u_df)
cat('\n\n')
fitCopula(tCopula(dim=2), data=u_df)
cat('\n\n')
fitCopula(gumbelCopula(dim=2), data=u_df)

Call: fitCopula(copula, data = data)
Fit based on "maximum pseudo-likelihood" and 3019 2-dimensional observations.
Copula: normalCopula 
rho.1 
0.439 
The maximized loglikelihood is 320.9 
Convergence problems: code is 52 see ?optim.

Call: fitCopula(copula, data = data)
Fit based on "maximum pseudo-likelihood" and 3019 2-dimensional observations.
Copula: tCopula 
    rho.1     df 
0.4327 4.6111 
The maximized loglikelihood is 372 
Optimization converged

Call: fitCopula(copula, data = data)
Fit based on "maximum pseudo-likelihood" and 3019 2-dimensional observations.
Copula: gumbelCopula 
alpha 
1.361 
The maximized loglikelihood is 291.7 
Optimization converged

A 2-dimensional t-copula has the following form:

where \(\nu\) and \(\rho\) are the degrees of freedom and correlation coefficient of the copula respectively.

Let’s fit a t copula with the fitted parameters from above (\(\rho\)=0.4327, df=4.6111) and draw 100000 samples from it.

Then, again with the probability integeral transform, we transform the these Uniform samples back to their marginal distributions, which we have selected as t distributions as studied earlier. Since the quantile \(q_i\) of sampled t copula variate \(u_i\) with its corresponding marginal df is in the form \(q_i=\frac{r_i-m}{s}\), the marginal variates will be adjusted accordingly by its specificed location and scale: \(r_i=q_i\times s+m\).

t_cop_fit_est <- fitCopula(tCopula(dim=2), data=u_df)@estimate
t_cop_fit_rho <- t_cop_fit_est[1]
t_cop_fit_df <- t_cop_fit_est[2]
t_cop <- tCopula(t_cop_fit_rho, df=t_cop_fit_df)
t_cop_samples <- rCopula(1e5, copula=t_cop)

t_cop_aapl <- qt(t_cop_samples[,1], df=aapl_df) * aapl_s + aapl_m
t_cop_gs <- qt(t_cop_samples[,2], df=gs_df) * gs_s + gs_m

Tail Dependence with Copula

With the generated marginal samples, we can now calculate tail depedence using the method we saw earlier.

tally2 <- matrix(0, 3, 7)
for (i in 1:7){
    q = probs[i]
    tally2[,i] = c(
        (sum((df[,1]<quantile(df[,1], q))*(df[,2]<quantile(df[,2], q))) / 
         sum((df[,1]<quantile(df[,1], q)))),
        (sum((mvn_samples[,1]<quantile(mvn_samples[,1], q)) * 
             (mvn_samples[,2]<quantile(mvn_samples[,2], q))) 
         / sum((mvn_samples[,1]<quantile(mvn_samples[,1], q)))),
        (sum((t_cop_aapl<quantile(t_cop_aapl, q))*(t_cop_gs<quantile(t_cop_gs, q))) / 
         sum((t_cop_aapl<quantile(t_cop_aapl, q))))
    )
}

tally2_df <- as.data.frame(tally2, row.names=c('observed',
                                               'normal', 
                                               't copula'))
colnames(tally2_df) <- as.character(probs)
print(tally2_df)

               0.2       0.1     0.05      0.02      0.01  0.005 0.001
observed 0.4668874 0.4337748 0.397351 0.3114754 0.3225806 0.1875  0.50
normal   0.4176500 0.3066000 0.218000 0.1570000 0.1130000 0.0800  0.07
t copula 0.4217500 0.3365000 0.293800 0.2590000 0.2380000 0.2440  0.23

It is also possible to calculate the tail dependence of copulas by \(\lambda=\lim_{q\rightarrow0^+}\frac{C(q,q)}{q}\). Substituting the expression for 2-dimensional t-copula and taking the limit, the tail dependence of t copula can be expressed as

2-2*(pt(sqrt(t_cop_fit_df+1)*sqrt(1-t_cop_fit_rho)/
        sqrt(1+t_cop_fit_rho), 
        df=t_cop_fit_df+1))

0.190010784498546

Although empirically at \(q=0.02\) and \(q=0.01\) the estimated tail dependence is close to the theoretical value of 0.19, at even lower probabilities, they start to increase. This could be due to insufficient data (we only have \(n=3019\) in the 12-year period) at the extremes resulting in inaccurate proportions.

Compared to simulated data from the bivariate normal distribution earlier, the simulation from the t copula is closer to the empirical data and produce substantial estimates at the tail, albeit still lower. In extreme cases like \(q=0.005\) or \(q=0.001\), we still manage to obtain estimates of tail dependence where it is too small for the bivariate normal to reliably estimate.

In the event of insufficiency of data, copulas are also able to provide a theoretical measure of tail dependence. It is however noteworthy that not all copulas model tail dependences. t copula provides the above formula for both lower and upper tail dependences, while Gumbel copula, for example, only models upper tail dependence.

Cover image: Karine Avetisyan (Unsplash)